Giải toán bằng phương pháp tọa độ

Giải toán bằng phương pháp tọa độ.

1. Xây dựng hệ tọa độ

Xây dựng hệ tọa độ hợp lý là điều rất cần thiết cho việc ứng dụng của phương pháp tọa độ trong việc giải toán. Đây là bước đầu tiên của bài giải. Người giáo viên cần hướng dẫn khéo léo giúp học sinh nhận ra các tính chất đặc biệt của bài toán, ở đây chủ yếu là sử dụng tính vuông góc, để xây dựng một hệ tọa độ mà trên đó các tham số được giảm một cách tối ưu nhất.

Ở đây, ta xem xét một số trường hợp áp dụng tốt phương pháp này.

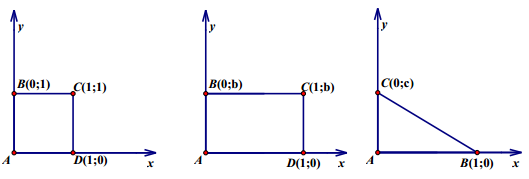
Đối với các bài toán có một trong các tứ giác như: hình vuông, hình chữ nhật, tam giác vuông. Đối với các hình như vậy ta có thể chọn hệ trục tọa độ có gốc nằm tại một đỉnh vuông, có hai trục Ox và Oy chứa 2 cạnh tương ứng của góc vuông đó. Và chọn đơn vị trên các trục bằng độ dài của một trong hai cạnh góc vuông. Bằng cách chọn như vậy, các tham số được giảm tối đa có thể. Và dạng hình này cũng là dạng áp dụng thuận lợi nhất phương pháp tọa độ trong mặt phẳng này.

Đối với các bài toán có chứa tam giác đều, tam giác cân, tam giác thường. Ta có thể xây dựng một hệ trục bằng cách dựa vào đường cao. Cụ thể, ta dựng đường cao từ một đỉnh bất kỳ (đối với tam giác cân ta nên dựng đường cao từ đỉnh cân). Chân đường cao khi đó chính là góc tọa độ, cạnh đáy và đường cao vừa dựng nằm trên hai trục tọa độ.

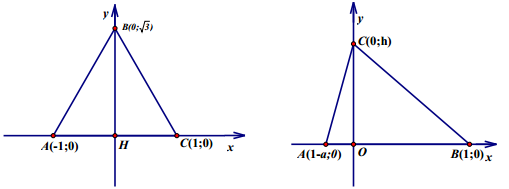
Đối với các bài toán có chứa các đường tròn thì ta có thể chọn góc tọa độ nằm tại tâm của đường tròn và đơn vị của hệ tọa độ bằng bán kính đường tròn, một hoặc hai trục chứa bán kính, đường kính của đường tròn.

Tuy nhiên, khi áp dụng thì không cứng nhắc trong việc chọn hệ trục tọa độ. Nên để học sinh linh hoạt và tìm ra cách chọn tối ưu cho bài toán.

Một số bài toán có thể có nhiều đối tượng hình học trên đó, thì tùy vào giả thuyết ta chọn hệ trục tọa độ cho phù hợp.

Download tài liệu Giải toán bằng phương pháp tọa độ tại đây: