Lý thuyết và bài tập giá trị lượng giác của một góc từ 0 đến 180 độ
A- Lý thuyết lượng giác của góc từ 0 đến 180 độ
1. Định nghĩa
Lấy M trên nửa đường tròn đơn vị tâm O. Xét góc nhọn α = $latex \widehat{xOM}$ . Giả sử M(x; y).
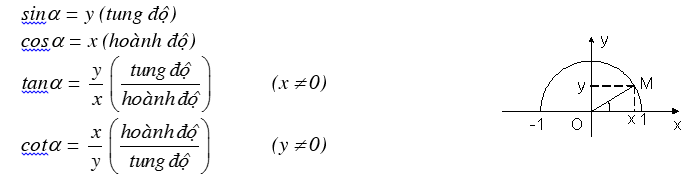
Chú ý:
– Nếu α tù thì cosα < 0, tanα < 0, cotα < 0.
– tana chỉ xác định khi α ≠ 900, cotα chỉ xác định khi a ≠ 00 và a ≠ 1800.
2. Tính chất
- Góc phụ nhau
$latex \begin{array}{l}\sin ({{90}^{0}}-\alpha )=\cos \alpha \\\cos ({{90}^{0}}-\alpha )=\sin \alpha \\\tan ({{90}^{0}}-\alpha )=\cot \alpha \\\cot ({{90}^{0}}-\alpha )=\tan \alpha \end{array}$
- Góc bù nhau
$latex \begin{array}{l}\sin ({{180}^{0}}-\alpha )=\sin \alpha \\\cos ({{180}^{0}}-\alpha )=-\cos \alpha \\\tan ({{180}^{0}}-\alpha )=-\tan \alpha \\\cot ({{180}^{0}}-\alpha )=-\cot \alpha \end{array}$
3. Giá trị lượng giác của các góc đặc biệt
| 00 | 300 | 450 | 600 | 900 | 1800 | |
| sinα | 0 | $latex \frac{1}{2}$ | $latex \frac{\sqrt{2}}{2}$ | $latex \frac{\sqrt{3}}{2}$ | 1 | 0 |
| cosα | 1 | $latex \frac{\sqrt{3}}{2}$ | $latex \frac{\sqrt{2}}{2}$ | $latex \frac{1}{2}$ | 0 | –1 |
| tanα | 0 | $latex \frac{\sqrt{3}}{3}$ | 1 | $latex \sqrt{3}$ | || | 0 |
| cotα | || | $latex \sqrt{3}$ | 1 | $latex \frac{\sqrt{3}}{3}$ | 0 | || |
4. Các hệ thức cơ bản
$latex \tan \alpha =\frac{\sin \alpha }{\cos \alpha }\,\,\,\,(\cos \alpha \ne 0)$ ;
$latex \cot \alpha =\frac{\cos \alpha }{\sin \alpha }\,\,\,\,(\sin \alpha \ne 0)$ ;
$latex \tan \alpha .\cot \alpha =1\,\,(\sin \alpha .\cos \alpha \ne 0)$ ;
$latex {{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1$ ;
$latex 1+{{\tan }^{2}}\alpha =\frac{1}{{{\cos }^{2}}\alpha }\,\,(\cos \alpha \ne 0)$ ;
$latex 1+{{\cot }^{2}}\alpha =\frac{1}{{{\sin }^{2}}\alpha }\,\,\,(\sin \alpha \ne 0)$ ;
B- Bài tập giá trị lượng giác của góc từ 0 đến 180 độ
Bài 1: Tính giá trị các biểu thức sau:
a) $latex \displaystyle a\sin {{0}^{0}}+b\cos {{0}^{0}}+c\sin {{90}^{0}}$
b) $latex \displaystyle a\cos {{90}^{0}}+b\sin {{90}^{0}}+c\sin {{180}^{0}}$
c) $latex \displaystyle {{a}^{2}}\sin {{90}^{0}}+{{b}^{2}}\cos {{90}^{0}}+{{c}^{2}}\cos {{180}^{0}}$
d) $latex 3-{{\sin }^{2}}{{90}^{0}}+2{{\cos }^{2}}{{60}^{0}}-3{{\tan }^{2}}{{45}^{0}}$
e) $latex 4{{a}^{2}}{{\sin }^{2}}{{45}^{0}}-3{{(a\tan {{45}^{0}})}^{2}}+{{(2a\cos {{45}^{0}})}^{2}}$
Bài 2: Tính giá trị các biểu thức sau:
a) sin x + cos x khi x bằng 00; 450; 600
b) 2sin x + cos 2x khi x bằng 450; 300.
Bài 3: Cho biết một giá trị lượng giác của một góc, tính các giá trị lượng giác còn lại:
a) $latex \sin \beta =\frac{1}{4}$ , β nhọn
b) $latex \cos \alpha =-\frac{1}{3}$
c) $latex \tan x=2\sqrt{2}$
Bài 4: Biết $latex \sin {{15}^{0}}=\frac{\sqrt{6}-\sqrt{2}}{4}$ . Tính $latex \cos {{15}^{0}},\,\,\tan {{15}^{0}},\,\,\cot {{15}^{0}}$
Bài 5: Cho biết một giá trị lượng giác của một góc, tính giá trị của một biểu thức:
a) $latex \sin x=\frac{1}{3},\,\,{{90}^{0}}<x<{{180}^{0}}$ . Tính $latex A=\frac{\tan x+3\cot x+1}{\tan x+\cot x}$
b) $latex \tan \alpha =\sqrt{2}$ . Tính $latex B=\frac{\sin \alpha -\cos \alpha }{{{\sin }^{3}}\alpha +3{{\cos }^{3}}\alpha +2\sin \alpha }$
Bài 6: Chứng minh các đẳng thức sau:
a) $latex {{(\sin x+\cos x)}^{2}}=1+2\sin x.\cos x$
b) $latex {{\sin }^{4}}x+{{\cos }^{4}}x=1-2{{\sin }^{2}}x.{{\cos }^{2}}x$
c) $latex {{\tan }^{2}}x-{{\sin }^{2}}x={{\tan }^{2}}x.{{\sin }^{2}}x$
d) $latex {{\sin }^{6}}x+{{\cos }^{6}}x=1-3{{\sin }^{2}}x.{{\cos }^{2}}x$
e) $latex \sin x.\cos x(1+\tan x)(1+\cot x)=1+2\sin x.\cos x$
Bài 7: Đơn giản các biểu thức sau:
a) $latex \cos y+\sin y.\tan y$
b) $latex \sqrt{1+\cos b}.\sqrt{1-\cos b}$
c) $latex \sin a\sqrt{1+{{\tan }^{2}}a}$
d) $latex \frac{1-{{\cos }^{2}}x}{1-{{\sin }^{2}}x}+\tan x.\cot x$
e) $latex \frac{1-4{{\sin }^{2}}x.{{\cos }^{2}}x}{{{(\sin x+\cos x)}^{2}}}$
f) $latex \sin ({{90}^{0}}-x)+\cos ({{180}^{0}}-x)+{{\sin }^{2}}x(1+{{\tan }^{2}}x)-{{\tan }^{2}}x$
Bài 8: Tính giá trị các biểu thức sau:
a) $latex {{\cos }^{2}}{{12}^{0}}+{{\cos }^{2}}{{78}^{0}}+{{\cos }^{2}}{{1}^{0}}+{{\cos }^{2}}{{89}^{0}}$
b) $latex {{\sin }^{2}}{{3}^{0}}+{{\sin }^{2}}{{15}^{0}}+{{\sin }^{2}}{{75}^{0}}+{{\sin }^{2}}{{87}^{0}}$
