Phương pháp chứng minh hai mặt phẳng vuông góc

Để chứng minh hai mặt phẳng vuông góc với nhau, các em cần hiểu rõ các khái niệm và cách xác định về góc giữa hai  mặt phẳng.

*Sơ qua về lý thuyết góc giữa 2 mặt phẳng:

– Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó

– Nếu hai mặt phẳng song song hoặc trùng nhau thì ta nói rằng góc giữa hai mặt phẳng đó bằng 0.

– Cách xác định góc giữa 2 mặt phẳng:

+ Giả sử hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến d. Từ một điểm I bất kì trên d ta dựng trong (P) đường thẳng a vuông góc với d và dựng trong (Q) đường thẳng b vuông góc với d.

Người ta đã chứng minh được góc giữa hai mặt phẳng (P) và (Q) là góc giữa hai đường thẳng a và b. Và mp (P) vuông góc với mp (Q) khi đường thẳng a vuông góc với đường thẳng b . Kí hiệu vuông góc: (P) ⊥ (Q)

*Tuy nhiên thực tế để chứng minh hai mặt phẳng vuông góc với nhau người ta sử dụng các định lý và hệ quả dưới đây để chứng minh:

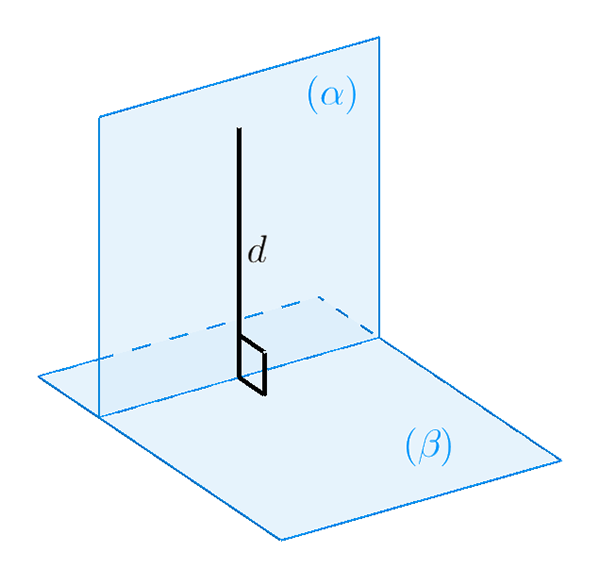
– Định lí 1: Điều kiện cần và đủ để hai mặt phẳng vuông góc với nhau là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

Hệ quả 1: Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này mà vuông góc với giao tuyến thì vuông góc với mặt phẳng kia.

Hệ quả 2: Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Nếu từ một điểm thuộc mặt phẳng (P) ta dựng một đường thẳng vuông góc với mặt phẳng (Q) thì đường thẳng này nằm trong mặt phẳng (P).

– Định lí 2: Nếu hai mặt phẳng cắt nhau và cùng vuông góc với một mặt phẳng thì giao tuyến của chúng vuông góc với mặt phẳng đó.

Phương pháp thường sử dụng để chứng minh 2 mặt phẳng vuông góc:

d ∈ (α) và d ⊥ (β) => (α) ⊥ (β)