Chuyên đề: Lũy thừa – Logarit và bài tập áp dụng

Lũy thừa – Logarit không chỉ là một chuyên đề trong nội dung toán lớp 12 mà còn xuất hiện trong nội dung kiến thức ôn tập và trong đề thi tốt nghiệp THPT.

• 18 câu trắc nghiệm lũy thừa, hàm số lũy thừa
• 63 bài toán ứng dụng hàm số mũ – lôgarit
• 50 câu trắc nghiệm phương trình mũ hay

Chuyên đề: Lũy thừa – Logarit và bài tập áp dụng

Bài viết dưới đây sẽ giúp các học sinh có thể tổng hợp lại tất cả các hệ thống kiến thức về chuyên đề Lũy thừa – Logarit và bài tập áp dụng có lời giải chi tiết, thuận lợi hơn trong việc học và ôn tập chuẩn bị cho kỳ thi tốt nghiệp THPT sắp đến.

Tóm tắt lý thuyết về chuyên đề Lũy thừa – Logarit

1. Lũy thừa

Khái niệm về lũy thừa

+ Lũy thừa với số mũ nguyên: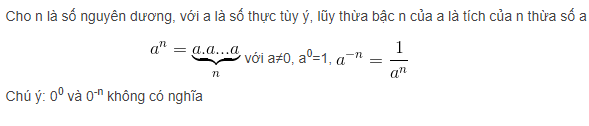 
+ Lũy thừa căn bậc n: Cho số thực b và số nguyên dương n (n≥2). Số a được gọi là căn bậc n của số b nếu aⁿ =b.

+ Lũy thừa với số mũ hữu tỉ: 

Lưu ý: khi xét lũy thừa với số mũ hữu tỉ, ta chỉ xét cơ số a dương.

Một số tính chất về lũy thừa

+ Tính chất 1: Về lũy thừa

Lưu ý:  Khi xét lũy thừa với số mũ nguyên các tính chất trên vẫn đúng khi cơ số a là một số thực tùy ý.

+ Tính chất 2: Về căn bậc n

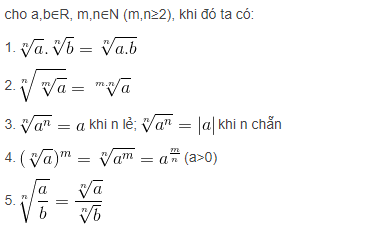
Lưu ý: Nếu số mũ m,n là số chẵn thì cơ số a, b phải thỏa mãn để căn thức có nghĩa.

+ Tính chất 3: So sánh 2 lũy thừa

Cho a∈R; m,n∈Z. Khi đó:

• Với a>1 thì a^m > aⁿ khi và chỉ khi m>n
• Với 0<a<1 thì a^m > aⁿ khi và chỉ khi m<n

Hệ quả
Với 0<a<b và m là số nguyên thì:

• a^m < aⁿ khi và chỉ khi m>0
  a^m > aⁿ khi và chỉ khi m<0

2. Logarit

Khái niệm về Logarit

Theo giảng viên Trường Trung học phổ thông Sài Gòn cho biết một số khái niệm về Logarit như sau:

+ Logarit cơ số a của b:

Nhận xét: Không có Logarit của số âm và số 0; Cơ số của Logarit phải dương và khác 1

+ Logarit thập phân: Logarit thập phân là logarit cơ số 10, ký hiệu logb

+ Logarit tự nhiên: Logarit tự nhiên là logarit cơ số e, ký hiệu lnb

Một số tính chất về Logarit

+ Tính chất 1: Quy tắc tính Logarit

Lưu ý: Các số a, b, c trong công thức phải thỏa mãn để Logarit có nghĩa.

+ Tính chất 2: So sánh 2 logarit cùng cơ số

Cho a>1, a≠0 và b,c>0:

• Khi a>1 thì log_ab > log_ac ⇔ b>c
• Khi 0<a<1 thì log_ab > log_ac ⇔ b<c

Hệ quả:

Cho a>1, a≠0 và b,c>0

• log_ab > 0 ⇔ a và b cùng lớn hơn 1 hoặc cùng nhỏ hơn 1
• log_ab = log_ac ⇔ b=c

+ Tính chất 3: So sánh 2 logarit khác cơ số

Nếu 0<1<b<1 hoặc 1<a<b thì:

• log_ax > log_bx ⇔ x>1
• log_ax < log_bx ⇔ 0<x<1

Một số bài tập áp dụng chuyên đề Lũy thừa – Logarit

Sau đây là một số bài tập vận dụng chuyên đề Lũy thừa – Logarit, các em học sinh cùng nhau thử sức nhé!

Hy vọng với bài viết này sẽ giúp các em ôn tập thật tốt, hoàn thành kỳ thi tốt nghiệp THPT và tuyển sinh Đại học – Cao đẳng đạt được kết quả như mong muốn! Chúc các em thành công

Nguồn: toancap3.com tổng hợp