Sơ đồ khảo sát và vẽ đồ thị hàm số bậc 3

Ở bài trước các em đã được học về sơ đồ chung về khảo sát và vẽ đồ thị hàm số. Với hàm số bậc 3 các em cũng làm với các bước đó.

SƠ ĐỒ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ BẬC BA: [latex]\displaystyle y=ax_{{}}^{3}+bx_{{}}^{2}+cx+d[/latex] (a # 0) .

1. Tập xác định: D = R

2. Sự biến thiên

– Xét chiều biến thiên của hàm số

+ Tính đạo hàm: y’

+ Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.

– Tìm cực trị

– Tìm các giới hạn tại vô cực ([latex]\displaystyle x\to \pm \infty [/latex])

Chú ý: Hàm số bậc 3 và các hàm đa thức không có tiệm cận đứng và tiệm cận ngang

– Lập bảng biến thiên: Cần phải thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.

3. Đồ thị của hàm số bậc 3

– Giao của đồ thị với trục tung (Oy): x=0 =>y= d => (0; d)

– Giao của đồ thị với trục hoành (Ox): y = 0 <=> [latex]\displaystyle y=ax_{{}}^{3}+bx_{{}}^{2}+cx+d[/latex] <=> x = ?

– Các điểm cực tiểu, cực đại nếu có.

– Lấy thêm một số điểm để hình dung ra hình dạng của đồ thị

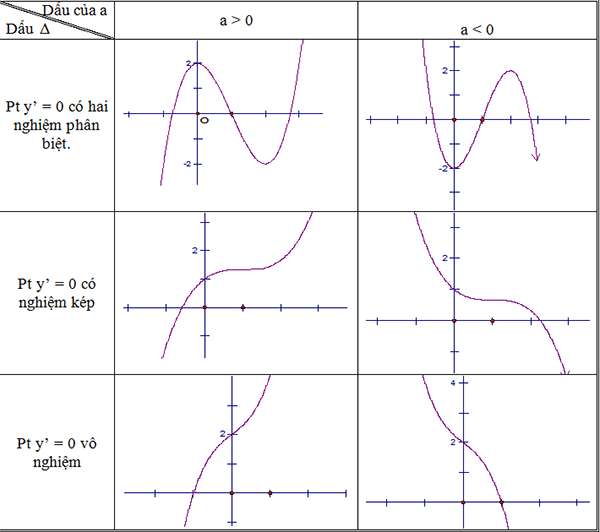
– Nhận xét về đặc trưng của đồ thị: Hàm bậc ba nhận điểm I làm tâm đối xứng.

+ Trong đó: [latex]\displaystyle {{x}_{0}}[/latex] là nghiệm của phương trình y’’ = 0 (đạo hàm cấp hai bằng 0)

+ Điểm I được gọi là ‘điểm uốn’ của đồ thị hàm số.

Các dạng đồ thị hàm số bậc 3: [latex]\displaystyle y=ax_{{}}^{3}+bx_{{}}^{2}+cx+d[/latex] (a # 0)

Ví dụ thực hành: khảo sát và vẽ đồ thị hàm số bậc 3: [latex]\displaystyle y=x_{{}}^{3}+3x_{{}}^{2}-4[/latex]

1. Tập xác định: D = R

2. Sự biến thiên

– Giới hạn hàm số tại vô cực

[latex]\displaystyle \underset{{x\to +\infty }}{\mathop{{\lim }}}\,y=+\infty ;\underset{{x\to -\infty }}{\mathop{{\lim }}}\,y=-\infty [/latex]

– Chiều biến thiên:

[latex]\displaystyle y’=3x_{{}}^{2}+6x[/latex]

Cho y’ = 0 <=> [latex]\displaystyle y’=3x_{{}}^{2}+6x[/latex] = 0 <=> [latex]\displaystyle \left[ \begin{array}{l}x=0\\x=-2\end{array} \right.[/latex]

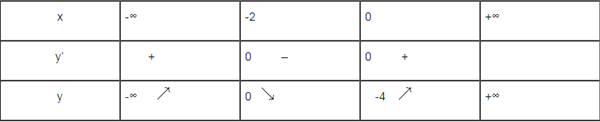
Hàm số nghịch biến trong khoảng (-2; 0)

Hàm số đồng biến trong khoảng (-∞; -2) và (0; +∞)

– Cực trị:

Hàm số đạt cực đại tại x = -2; [latex]\displaystyle {{y}_{{CD}}}[/latex] = y(-2) = 0

Hàm số đạt cực tiểu tại x = 0; [latex]\displaystyle {{y}_{{CT}}}[/latex]=y(0) = -4

– Lập bảng biến thiên

3. Đồ thị của hàm số (C)

Vẽ đồ thị (C) :

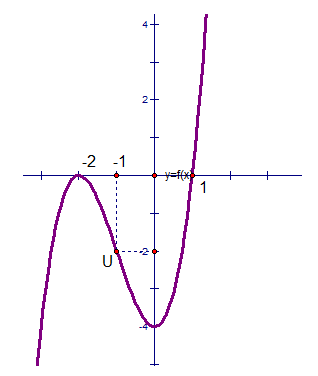
Đồ thị của hàm số bậc 3 đã cho nhận điểm U (-1;-2) làm tâm đối xứng.