Phương pháp chứng minh 3 điểm thẳng hàng trong không gian
Toancap3.com giới thiệu các em phương pháp chứng minh 3 điểm thẳng hàng trong không gian với cách làm đầy đủ dưới đây. Cụ thể qua các ví dụ.
Nội dung chính của phương pháp là ta sẽ chứng minh cho 3 điểm thuộc giao tuyến của hai mặt phẳng phân biệt.
Phương pháp cần dùng: Cách tìm giao điểm của đường thẳng và mặt phẳng trong không gian
Chúng ta cùng xét ví dụ dưới đây:
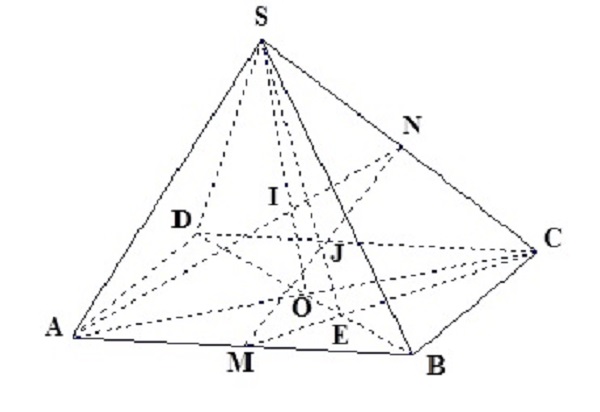
Ví dụ 1: Cho hình bình hành ABCD và S là điểm không thuộc (ABCD), M và N lần lượt là trung điểm của AB và SC .
a, Xác định giao điểm I = AN ∩ (SBD)
b, Xác định giao điểm J = MN ∩(SBD)
c, Chứng minh 3 điểm B, I, J thẳng hàng
Lời giải:
1. Xác định giao điểm I = AN ∩ (SBD )
Chọn mp phụ (SAC) ⊃ AN
Tìm giao tuyến của (SAC ) và (SBD)
( SAC) ∩ (SBD) = SO
Trong (SAC), gọi I = AN ∩ SO
I ∈ AN
I ∈ SO mà SO ∈ ( SBD) → I ∈ ( SBD)
Vậy: I = AN ∩ ( SBD)
2. Xác định giao điểm J = MN ∩ (SBD)
Chọn mp phụ (SMC) ∩ MN
Tìm giao tuyến của (SMC ) và (SBD)
S là điểm chung của (SMC ) và (SBD)
Trong (ABCD) , gọi E = MC ∩ BD
→ ( SAC) ∩ (SBD) = SE
Trong (SMC), gọi J = MN ∩ SE
J∈ MN
J∈ SE mà SE ∈ ( SBD) → J ∈ ( SBD)
Vậy J = MN ∩( SBD)
2. Chứng minh B, I, J thẳng hàng
Ta có : B là điểm chung của (ANB) và ( SBD)
I ∈ SO mà SO ∈ ( SBD) → I ∈ ( SBD)
I ∈ AN mà AN∈ (ANB) → I ∈ (ANB)
→ I là điểm chung của (ANB) và ( SBD)
J ∈ SE mà SE ∈ ( SBD) → J ∈ ( SBD)
J ∈ MN mà MN ∈ (ANB) → J ∈ (ANB)
→ J là điểm chung của (ANB) và ( SBD)
Vậy : B, I, J thẳng hàng
Tương tự các em làm tiếp các ví dụ dưới đây:
Ví dụ 2: Cho tứ giác ABCD và S ∉ (ABCD). Gọi I, J là hai điểm trên AD và SB , AD cắt BC tại O và OJ cắt SC tại M.
Tìm giao điểm K = IJ và (SAC)
Xác định giao điểm L = DJ và (SAC)
Chứng minh A, K, L, M thẳng hàng
Ví dụ 3: Cho tứ diện SABC. Gọi L, M, N lần lượt là các điểm trên các cạnh SA, SB và AC sao cho LM không song song với AB, LN không song song với SC.
Tìm giao tuyến của mp (LMN) và (ABC)
Tìm giao điểm I = BC ∩( LMN) và J = SC ∩ ( LMN)
Chứng minh M, I, J thẳng hàng
Khi giải xong các ví dụ trên chắc chắn các em sẽ nắm chắc được cách chứng minh 3 điểm thẳng hàng trong không gian rồi. Theo dõi các bài viết tiếp theo thuộc chuyên đề Hình không gian nhé.