Áp dụng định lý Côsin trong tam giác vào giải Toán
Bài viết này nêu ra những ứng dụng và cách áp dụng định lý Côsin trong tam giác vào giải Toán.
Trước tiên chúng ta sẽ nhắc lại lý thuyết về định lý Côsin.
Tóm tắt
I – Lý thuyết về định lý Cosin
1. Định lý Côsin
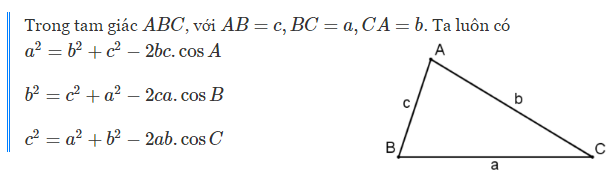
Ý nghĩa của định lý Cosin: Trong một tam giác, ta luôn tính được cạnh thứ ba nếu biết hai cạnh và góc xen giữa.
2. Hệ quả của định lý Cosin
Trong một tam giác, ta luôn tính được các góc nếu biết 3 cạnh.
Trong tam giác ΔABC có các cạnh AB = c, BC = a, CA = b
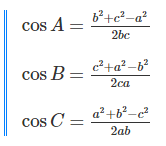
II – Bài tập áp dụng định lý Cosin trong tam giác
Ví dụ 1: Cho tam giác ΔABC, có AB =c ,BC = a,CA = b và M là trung điểm của BC. Tính độ dài đường trung tuyến AM theo a,b và c.
Giải
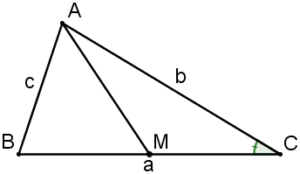
Xét ΔACM áp dụng định lý cosin vào tam giác này:
Ta có:
$latex \displaystyle AM_{{}}^{2}=CA_{{}}^{2}+CM_{{}}^{2}-2.CA.CM.cos\widehat{ACM}=b_{{}}^{2}+\frac{a_{{}}^{2}}{4}-b.a.cos\widehat{ACM}$ (1)
Áp dụng hệ quả của định lý cosin vào tam giác ΔABC:
$latex \displaystyle cos\widehat{ACB}=cos\widehat{ACM}=\frac{CA_{{}}^{2}+CB_{{}}^{2}}{2.CA.CB}=\frac{b_{{}}^{2}+a_{{}}^{2}-c_{{}}^{2}}{2ba}$ (2)
Thay (2) vào (1):
$latex \displaystyle AM_{{}}^{2}=b_{{}}^{2}+\frac{a_{{}}^{2}}{4}-b.a.\frac{b_{{}}^{2}+a_{{}}^{2}-c_{{}}^{2}}{2ba}=\frac{b_{{}}^{2}}{2}+\frac{c_{{}}^{2}}{2}-\frac{a_{{}}^{2}}{2}$
