03/04/2017
Lý thuyết về giới hạn của hàm số
Lý thuyết về giới hạn của hàm số
Tóm tắt
1. Giới hạn hữu hạn
+) Cho khoảng K chứa điểm [latex]\displaystyle {{x}_{0}}[/latex] và hàm số y = f(x) xác định trên K hoặc trên K\{[latex]\displaystyle {{x}_{0}}[/latex]}.
[latex]\displaystyle \underset{x\to {{x}_{0}}}{\mathop{\lim }}\,f(x)=L[/latex] khi và chỉ khi với dãy số ([latex]\displaystyle {{x}_{n}}[/latex]) bất kì, [latex]\displaystyle {{x}_{n}}[/latex] ∈ K \{[latex]\displaystyle {{x}_{0}}[/latex]} và xn → [latex]\displaystyle {{x}_{0}}[/latex], ta có:
[latex]\displaystyle \underset{{}}{\mathop{\lim }}\,f({{x}_{n}})=L[/latex].

2. Giới hạn vô cực

3. Các giới hạn đặc biệt

4. Định lí về giới hạn hữu hạn
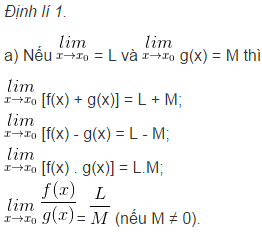
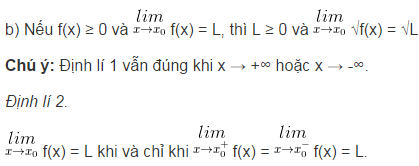
5. Quy tắc về giới hạn vô cực