20/06/2017
Một bài toán lượng giác hay
Toancap3.com xin chia sẻ một bài toán lượng giác hay. Bài viết được sưu tầm từ blog nguyenanhtuan2011.wordpress.com.
Cho và
Giải phương trình sau:
Lời giải 1: ( Theo maxmin )
DoVậy:
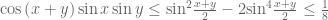
Lời giải 2: ( Theo longtoanlqc )
Không giảm tính tổng quát giả sử:(*) Xét hàm số:

,vì (*) và giải thiết ta suy ra được :
Suy ra
Do đó
nghịch biến, ta được:
Vì vậy từ pt ta suy ra
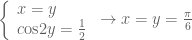
(Nguồn bài viết: nguyenanhtuan2011.wordpress.com)
