Bài thơ giúp nhớ các công thức bảng lượng giác môn Toán hiệu quả
Sau đây là bảng tóm tắt công thức lượng giác môn Toán được Toán cấp 3 sưu tầm nhằm giúp cho học sinh lớp 12, sĩ tử ôn thi đại học dễ hiểu, dễ nhớ hiệu quả.
- “Nguyên tắc vàng” trong ôn thi môn Toán THPT Quốc Gia năm 2020
- Để ôn thi THPT Quốc Gia môn Toán hiệu quả không nên bỏ qua 6 điều sau
- Cách chọn sách ôn thi THPT Quốc Gia môn Toán năm 2020 hiệu quả
Ôn thi môn Toán THPT Quốc Gia không bao giờ là dễ đặc biệt là nhớ Bảng công thức lượng giác, do đó đòi hỏi học sinh phải có sự cần cù, chăm chỉ, siêng năng học tập mới có thể đạt được thành tích cao. Để giúp các thí sinh có thể dễ dàng nhớ được các công thức của môn Toán, Toán cấp 3 sưu tầm đầy đủ các bảng công thức lượng giác, đầy đủ, dễ nhớ học sinh có thể tham khảo.
Tóm tắt
- 1 Công thức lượng giác của các cung liên quan đặc biệt
- 2 II. Công thức lượng giác cơ bản và công thức cộng
- 3 III. Công thức lượng giác nhân đôi, nhân ba và công thức hạ bậc
- 4 IV. Công thức lượng giác biến đổi tích thành tổng, tổng thành tích
- 5 V. Công thức nghiệm của phương trình lượng giác cơ bản
- 6 Bài thơ giúp nhớ các công thức bảng lượng giác môn Toán hiệu quả
- 6.1 Bài thơ về hàm số lượng giác
- 6.2 Bài thơ về giá trị lượng giác của các cung đặc biệt
- 6.3 Bài thơ về công thức cộng
- 6.4 Bài thơ về công thức nhân ba
- 6.5 Bài thơ về công thức gấp đôi
- 6.6 Bài thơ về công thức biến đổi tích thành tổng
- 6.7 Bài thơ về công thức biến đổi tổng thành tích
- 6.8 Bài thơ về công thức chia đôi (tính theo t = tg (a/2) )
- 6.9 Bài thơ về hệ thức lượng giác trong tam giác vuông
- 6.10 Bài thơ về diện tích
- 6.11 Khác
Công thức lượng giác của các cung liên quan đặc biệt

II. Công thức lượng giác cơ bản và công thức cộng

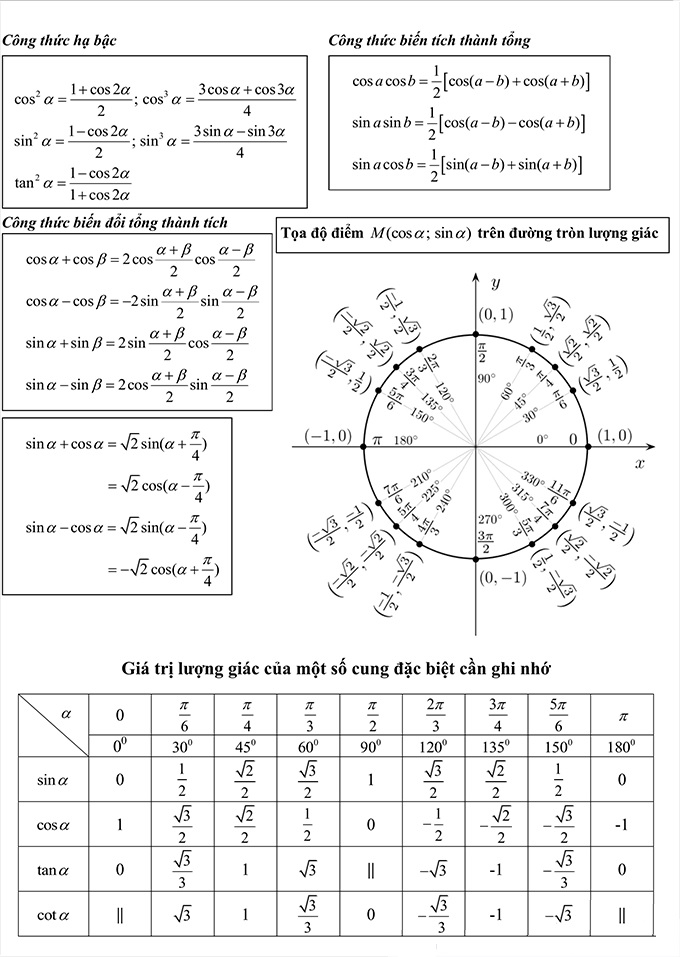
III. Công thức lượng giác nhân đôi, nhân ba và công thức hạ bậc

IV. Công thức lượng giác biến đổi tích thành tổng, tổng thành tích
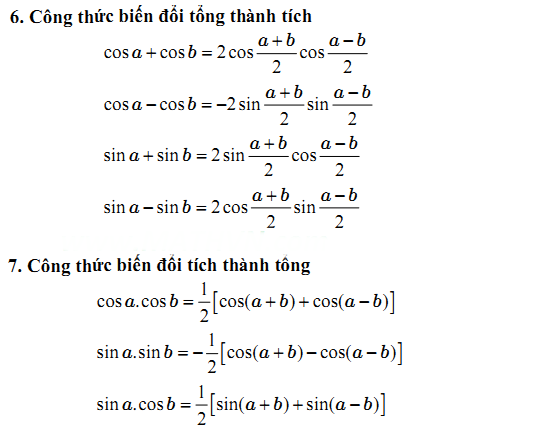
V. Công thức nghiệm của phương trình lượng giác cơ bản
Bài thơ giúp nhớ các công thức bảng lượng giác môn Toán hiệu quả
Theo giảng viên Trường Trung học phổ thông Sài Gòn chia sẻ: Để thuộc và nhớ lâu các công thức toán học, học sinh không nên học theo các học thuộc lòng như các môn học khác mà phải có chiến thuật học tập, đọc hiểu, khai thác và áp dụng tối đa các công thức. Vì thế, để môn học hấp dẫn cũng như để học sinh tiếp thu bài nhanh hơn, một số bài thơ về các công thức lượng giác đã ra đời. Chúng ta cùng tìm hiểu nhé!
Bài thơ về hàm số lượng giác
Bắt được quả TANG
SIN nằm trên COS (tan@ = sin@:cos@)
COTANG dại dột
Bị COS đè cho. (cot@ = cos@:sin@)
Hoặc
Bắt được quả tang
SIN nằm trên COS
COTANG cãi lại
COS nằm trên SIN!
Bài thơ về giá trị lượng giác của các cung đặc biệt
COS đối, SIN bù, phụ chéo, khác pi TAN
Nghĩa là:
- COSIN của hai góc đối bằng nhau
- SIN của hai góc bù nhau thì bằng nhau
- Phụ chéo là 2 góc phụ nhau thì SIN góc này = COS góc kia
- TAN góc này = COT góc kia
- TAN của hai góc hơn kém pi thì bằng nhau.
Bài thơ về công thức cộng
COS cộng COS bằng hai COS COS
COS trừ COS bằng trừ hai SIN SIN
SIN cộng SIN bằng hai SIN COS
SIN trừ SIN bằng hai COS SIN
Tóm lại:
SIN thì SIN COS COS SIN
COS thì COS COS SIN SIN “coi chừng” (dấu trừ).
TAN tổng thì lấy tổng TAN
Chia một trừ với tích TAN, dễ òm.
Bài thơ về công thức nhân ba
Nhân ba một góc bất kỳ
SIN thì ba bốn, COS thì bốn ba
Dấu trừ đặt giữa hai ta
Lập phương chỗ bốn … thế là ok.
Bài thơ về công thức gấp đôi
SIN gấp đôi = 2 SIN COS
COS gấp đôi = bình COS trừ bình SIN
Trừ 1 cộng hai lần bình COS
Cộng 1 trừ hai lần bình SIN
TAN gấp đôi
TAN đôi ta lấy đôi TAN (2 TAN)
Chia 1 trừ lại bình TAN, ra liền.
Nhớ công thức: tan (a + b)=(tan a + tan b)/1 – tan a . tan b bằng cách:
- TAN một tổng hai tầng cao rộng
- Trên thượng tầng tan cộng TAN TAN
- Dưới hạ tầng số 1 ngang tàng
- Dám trừ một tích TAN TAN oai hùng
Bài thơ về công thức biến đổi tích thành tổng
- COS COS nửa COS-cộng, cộng COS-trừ
- SIN SIN nửa COS-trừ trừ COS-cộng
- SIN COS nửa SIN-cộng cộng SIN-trừ
Bài thơ về công thức biến đổi tổng thành tích
SIN tổng lập tổng SIN cô
Cô tổng lập hiệu đôi cô đôi chàng
Còn TAN tử cộng đôi TAN (hoặc là: TAN tổng lập tổng hai TAN)
Một trừ TAN tích mẫu mang thương sầu
Gặp hiệu ta chớ lo âu
Đổi trừ thành cộng ghi sâu vào lòng
Hoặc:
Tan mình cộng với tan ta, bằng sin 2 đứa trên cos ta cos mình… nghĩa là:
- Tan x + Tan y: tình mình cộng lại tình ta, sinh ra hai đứa con mình con ta
- Tan x – Tan y: tình mình hiệu với tình ta sinh ra hiệu chúng, con ta con mình
Bài thơ về công thức chia đôi (tính theo t = tg (a/2) )
- SIN, COS mẫu giống nhau chả khác
- Ai cũng là một cộng bình tê (1 + t^2)
- SIN thì tử có hai tê (2t),
- COS thì tử có 1 trừ bình tê (1-t^2).
Bài thơ về hệ thức lượng giác trong tam giác vuông
- Sao Đi Học ( Sin = Đối / Huyền)
- Cứ Khóc Hoài ( Cos = Kề / Huyền)
- Thôi Đừng Khóc ( Tan = Đối / Kề)
- Có Kẹo Đây ( Cotan = Kề/ Đối)
- Sin : đi học (cạnh đối – cạnh huyền)
- Cos: không hư (cạnh đối – cạnh huyền)
- Tang: đoàn kết (cạnh đối – cạnh kề)
- Cotang: kết đoàn (cạnh kề – cạnh đối)
Nghĩa là:
- Tìm SIN lấy đối chia huyền
- COSIN lấy cạnh kề, huyền chia nhau
- Còn TANG ta hãy tính sau
- Đối trên, kề dưới chia nhau ra liền
- COTANG cũng dễ ăn tiền
- Kề trên, đối dưới chia liền là ra
SIN bù, COS đối, hơn kém pi TANG, phụ chéo.
- SIN bù :Sin(180-a)=sina
- COS đối :Cos(-a)=cosa
- Hơn kém pi TANG: Tg(a+180)=tga; Cotg(a+180)=cotga
- Phụ chéo là 2 góc phụ nhau thì SIN góc này = COS góc kia, TG góc này = COTG góc kia.
Công thức tổng quát hơn về việc hơn kém pi như sau:
- Hơn kém bội hai pi sin, cos
- Tang, cotang hơn kém bội pi.
- Sin(a+k.2.180)=sina ; Cos(a+k.2.180)=cosa
- Tg(a+k180)=tga ; Cotg(a+k180)=cotga
SIN bình + COS bình = 1
SIN bình = TG bình trên TG bình cộng 1.
COS bình = 1 trên 1 cộng TG bình.
Một trên COS bình = 1 cộng TG bình.
Một trên SIN bình = 1 cộng COTG bình.
Bài thơ về diện tích
Muốn tính diện tích hình thang
Đáy lớn, đáy bé ta mang cộng vào
Rồi đem nhân với đường cao
Chia đôi kết quả thế nào cũng ra.
Muốn tìm diện tích hình vuông,
Cạnh nhân với cạnh ta thường chẳng sai
Chu vi ta đã học bài,
Cạnh nhân với bốn có sai bao giờ.
Muốn tìm diện tích hình tròn,
Pi nhân bán kính, bình phương sẽ thành.
Nguyên tắc để 2 tam giác bằng nhau
Con gà con, gân cổ gáy, cúc cù cu
(cạnh góc cạnh, góc cạnh góc, cạnh cạnh cạnh)
Khác

Chúc các bạn ôn Toán vui vẻ và hiệu quả, đạt kết quả cao trong Kỳ thi THPT Quốc Gia và tuyển sinh Đại học – Cao đẳng năm 2020 sắp đến!
Nguồn: toancap3.com sưu tầm
