Hàm số bậc nhất y=ax+b
Lý thuyết cơ bản về hàm số bậc nhất y=ax+b
Tóm tắt
1. Khái niệm về hàm số bậc nhất
Hàm số bậc nhất là hàm số được cho bởi công thức: y = ax + b trong đó: a, b là các số cho trước và a ≠ 0.
2. Tính đồng biến và nghịch biến của hàm số bậc nhất
Hàm số bậc nhất y = ax + b ( với a ≠ 0) được xác định với mọi giá trị x ∈ R và có tính chất sau:
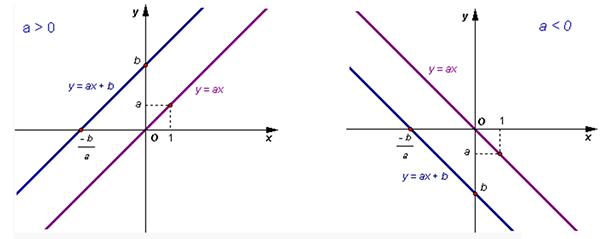
– Với a > 0 thì hàm số y = ax + b đồng biến trên R
– Với a < 0 thì hàm số y = ax + b nghịch biến trên R
3. Đồ thị của hàm số bậc nhất y = ax + b
a) Đồ thị hàm số y = ax + b (a ≠ 0)
b) Đồ thị hàm số y = ax (a ≠ 0)
c) Đồ thị hàm số y = |ax + b|
d) Các đồ thị hàm số đặc biệt: y = m, x = n (m, n ∈ R).
4) Hệ số góc của đường thẳng: y = ax + b (a ≠ 0)
Đường thẳng y = ax + b có hệ số góc là a
– Các tính chất hệ số góc:
+ Hai đường thẳng song song thì có hệ số góc bằng nhau.
+ Hai đường thẳng vuông góc với nhau thì có tích hệ số góc bằng -1
+ Đường thẳng y = ax + b ( với a > 0) tạo với tia Ox một góc α thì a = tanα
Phương trình đường thẳng đi qua A [latex] \displaystyle ({{x}_{0}};{{y}_{0}}) [/latex] và có hệ số góc k cho trước là: [latex] \displaystyle y=k(x-{{x}_{0}})+{{y}_{0}} [/latex]
